Imagine that we have billions of files and we would like to remove duplicates, i.e. find exact matches and keep only one of the multiple files. How would you do that? The simplest way is to generate hashes (e.g. md5 chechsums) of the files, compare them and keep only one file for each different hash. This is easily parallelizable and it will solve our problem in a very simple way. But what happens when we try to find near duplicates? E.g. consider setups where noise in our data is present, such as audio, image or video. Even news articles from different sources might talk about the exact same topic with the exact same information without being written on the exact way way. What we do in this case?<\p>

Locality Sensitive Hashing

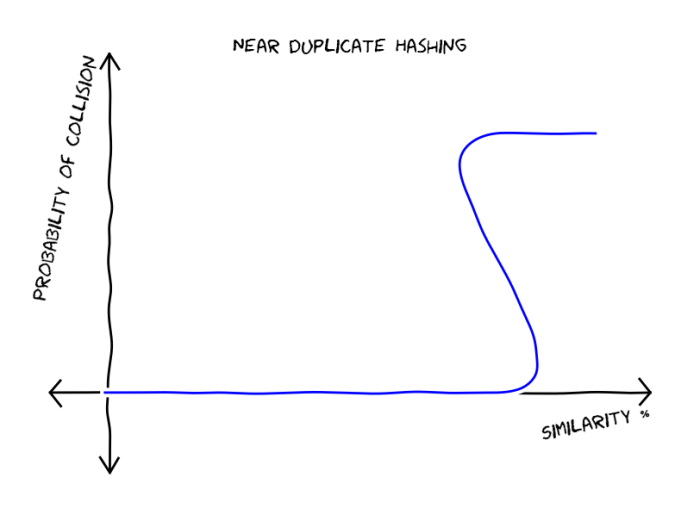
One way to find near duplicates would be to decide upon a threshold e.g. 80% and accept as duplicates the pairs of files that have similarity larger or equal to this threshold. This is a bad idea since it will require quadratic amount of effort. Ideally, we would like to have a hash function that takes the file, computes a hash value and this value would be equal for files that have similarity larger or equal to the threshold. As you see in the next figure the probability of having a collision is 0 below the threshold and equal to 1 when similarity reaches it.

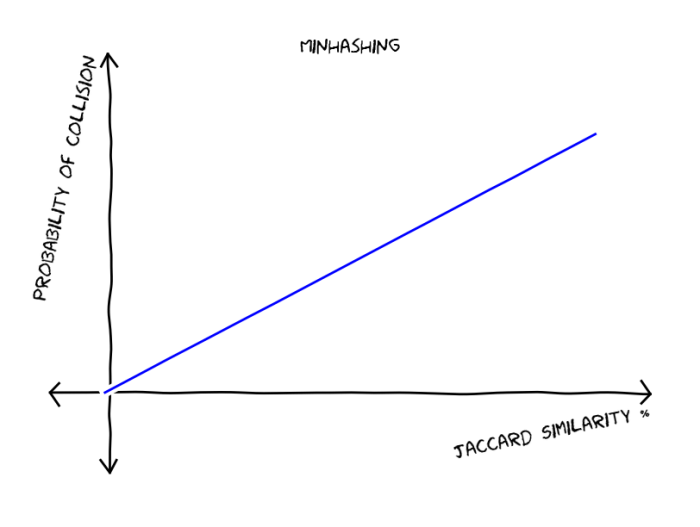
But how do we construct such a hash function? For our luck there are hashing function that can approximate certain similarity measures, for example Minhashing approximates Jaccard similarity and Random Hyperplanes approximates cosine similarity. For the particular case of the Minhashing, we have that the probability of two documents produce the same hash value is equal to their Jaccard similarity, making a linear graph that looks like this:

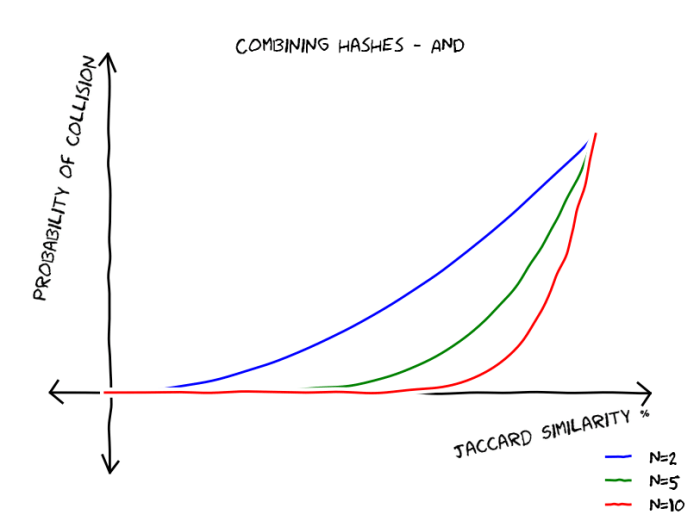
So, given the Minhash function, represented with the second graph, we would like to construct a hash function that would have a graph similar to the first one. Now lets do the following, we break our files into N chunks, we hash each chunk using Minhashing and we consider near duplicates the pairs that have collisions for all chunks. Since we have N independent events the probability of having collision to all chunks is equal to . As we can see by the following graph this trick reduced false positives but gave us more false negatives.

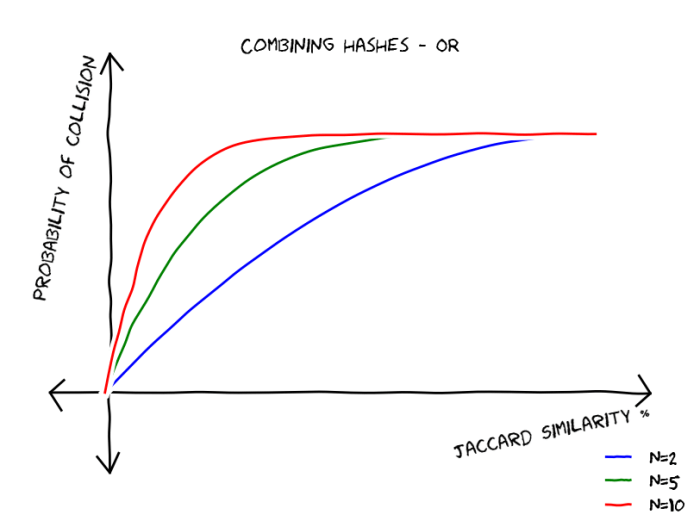
What if we accept a near duplicate if there is at least one chunk collision? The probability of none chunk colliding is , then the probability that at least one chunk collides is equal to . This gives us the following type of functions, these functions reduce false negatives but increase false positives.

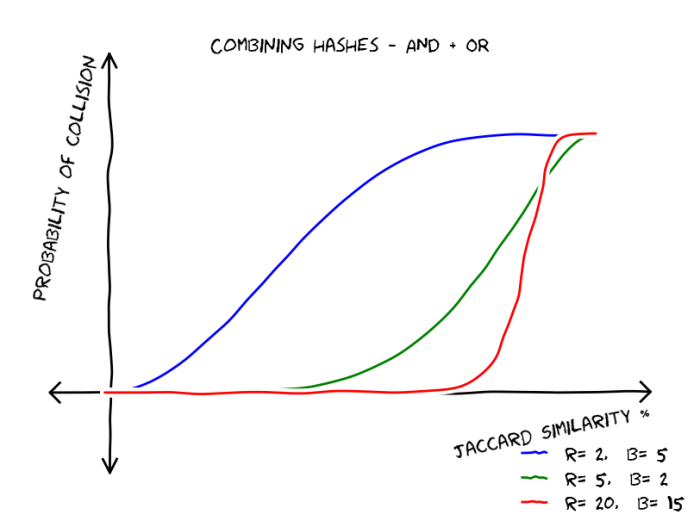
As we said AND combinations (all collisions) reduce false positives and OR combinations (at least one collision) reduce false negatives, the ideal is to get a hash strategy that reduces both false positives and false negatives, if we manage to do so, we will get a graph similar to the first one. The idea is straight-forward use both AND and OR combinations of hash functions, lets imagine that we have AND combinations followed by OR combinations. What does this mean? We break our files into chunks, lets say we have bands and each band has rows (or chunks). We hash each row using minhashing, we say that there is a collision in a particular band if each row in that band collide with the corresponding row from the same band in another file. If there is at least one band collision then we have a near duplicate. Lets see now how this procedure affects the collision probabilities. There is a collision in a particular band if all rows collide, therefore the probability for collision in that band is equal to . The probability of having zero band collisions is equal to , this makes the probability of having at least one band collision equal to . This gives the following graphs:

As you can see, the more combinations we do the more we reach to the desired hash funcion that resembles a step function that accepts as near duplicates those pairs that have similarity larger than a threshold. On the efficiency of this method: all we need to do is to run through all our files and generate hashes, then based on these hashes we can generate a list of files that collide in at least one band, and this list is our near duplicates, but using this technique we avoided to compare each file with each file, making the algorithm linear in the number of files and suitable deduplicating large amounts of data.

References
[1] Rajaraman, A.; Ullman, J. (2010). “Mining of Massive Datasets, Ch. 3.”.

 

This is my first blog post. The purpose of this blog is to share knowledge in the areas of Data Mining, Data Science, Databases, and Machine Learning, I will try to add interesting posts in a regular basis (e.g. 1 post per week or 2 weeks)!